Les
proportions dans les buffets d’orgue
Télécharger la version pdf (274 Ko)
Introduction
A l'époque où je débutais dans le métier de facteur
d'orgues, je pensais que les buffets anciens ne devaient leur beauté qu'à une
sorte d'inspiration chez leurs créateurs. La construction interne de leurs
dessins devait être inconsciente, ou simplement le produit du hasard.
C'est par une voie détournée que j'ai été amené à changer
d'avis. Je n'étais pas doué pour le dessin, mais il m'attirait quand même. J'ai
cherché alors à l'aborder par des méthodes intellectuelles. J'ai peu à peu
appris, au travers de lectures et d'autres renseignements, qu'on pouvait
construire un buffet d'orgue à l'aide de rapports géométriques, ou proportions.
J'ai même trouvé que cela rendait la tâche plus facile que je ne l'aurais
cru :
En analysant des buffets anciens, je me suis aperçu qu'ils
étaient construits sur une ou deux proportions (rarement plus). Les facteurs se
les imposaient à l'avance et ne les modifiaient plus au cours du dessin, un peu
comme un sujet de fugue. Au premier abord, on est tenté de croire à des
coïncidences, mais quand elles deviennent trop nombreuses, on est forcé
d'admettre qu'il s'agit d'une manière de faire déterminée et voulue chez les
anciens.
Définitions
Voyons ce que dit le dictionnaire du mot proportion :
« Convenance et rapport des parties entre elles et avec leur tout. »
Comment définit-on le rapport? Le rapport de deux
nombres est le quotient de leur division.
Pour le mot Harmonie, enfin : science des
accords; accord parfait entre les parties d'un tout.
Nous voyons que les définitions de la proportion et de
l'harmonie sont quasiment les mêmes. C'est cet « accord des parties entre
elles et avec leur tout » que les anciens semblent avoir tant recherché,
que ce soit en architecture, peinture, rhétorique, conceptions scientifiques,
musique, et bien sûr dans la construction des orgues.
L'une des origines de cette préoccupation dans la
civilisation occidentale est l'héritage de la pensée grecque. Les intellectuels
du Moyen-Age ont énormément étudié cette pensée (par exemple, la gamme musicale
qu'ils ont instaurée est directement inspirée du système Pythagoricien).
La Renaissance se voulait un retour aux sources antiques et
les références à la pensée grecque sont innombrables dans tous les arts de
cette époque. Les artistes étaient alors convaincus de refaire les choses comme
dans l'Antiquité (on faisait des tragédies dans le goût grec, des édifices à
l'Antique, etc.).
Le Baroque a encore puisé à la même source, en étant bien
étayé par l'héritage de la Renaissance.
Ce qui est frappant dans ces brèves considérations, c'est
que le regard des anciens semble avoir été tourné (au moins en partie) vers le
passé. Une telle attitude nous semble au premier abord rétrograde, car notre
époque veut le progrès, la croissance et la nouveauté à tout prix. Cependant,
réflexion faite, on peut se demander si ce n'est pas précisément cette attitude
qui donnait leur pouvoir créateur aux Anciens. Ils ne cherchaient pas du tout à
avoir des idées nouvelles, mais ils n'en manquaient pas non plus, c'est le
moins que l'on puisse dire. Paradoxalement, cette assise aussi ferme sur la
tradition semble avoir favorisé l'éclosion des idées, qui n'étaient pas
forcées, comme souvent aujourd'hui, mais venaient naturellement et à leur
heure.
Une idée très répandue chez les anciens était que l'harmonie
idéale, au sens le plus large du terme, reposait sur des proportions et
correspondait à notre être profond, dont la conscience est endormie. Platon dit
à ce sujet dans le Timée :
« Or l'harmonie est faite de mouvements de même nature
que les révolutions de l'âme en nous : et pour qui use avec intelligence
du commerce des Muses, ce n'est pas dans un plaisir irraisonné, comme le veut
l'opinion actuelle, que réside son utilité; mais comme de naissance, en nous la
révolutions de l'âme est inharmonique, c'est pour la mettre en ordre et en
accord avec soi que l'harmonie nous a été donné par les Muses ».
Cette citation nous montre que dans la pensée de Platon,
l'harmonie (avec elle les proportions et les nombres) est d'essence divine, et
que l'homme par son activité dans l'art recherche ce qui au fond de lui-même
est relié à la divinité, puisqu'il en est issu. Cette idée a inspiré et motivé
toute l'Antiquité et largement notre civilisation européenne en particulier le
Moyen-Age comme nous l'avons déjà vu.
Les nombres étaient considérés comme la base de toutes
choses. De ce fait, toutes les sciences étaient liées : rhétorique,
grammaire, musique, géométrie, philosophie, etc.. Loin de vouloir les séparer,
on cherchait leurs lois communes (par exemple: 2/3 est une fraction en
arithmétique, une proportion en géométrie, une quinte en musique et un rapport
de distances en astronomie). D'autre part, les nombreuses structures
géométriques qu'on trouve dans la nature faisaient dire aux anciens que Dieu
était géomètre. Dans un tel état d'esprit, on comprend que les artistes et les
artisans aient cultivé et utilisé la géométrie et l'art du compas (celui-ci
servant alors beaucoup plus à reporter des mesures qu'à faire des cercles) et
ceci pendant des millénaires.
Exemples
Voici ce qu'on entend par proportion dans la pratique :
une proportion est la comparaison d'une grandeur et d'une autre. Par exemple,
si je trace un segment de droite de longueur 1 et à côté de celui-ci un autre
de longueur double comme ceci :
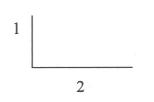
il y a entre ces deux longueurs un rapport de 2 : 1 ou 1 :
2. Comme on le voit, cette comparaison de deux grandeurs peut être exprimée par
une fraction (2/1 ou 1/2).
Les fractions étaient très utilisées dans la pratique des mesures;
on disait 1/4 ou 1/3 de pied, ou bien 2/3 ou 1/3 de telle ou telle longueur.
Elles servaient aussi dans les mathématiques, également pour des raisons pratiques :
ainsi, pour calculer le périmètre du cercle, on n’utilisait pas ![]() = 3.1415927 mais son
approximation 22/7 = 3.1428571.
= 3.1415927 mais son
approximation 22/7 = 3.1428571.
Revenons à nos deux segments. Si je trace un troisième
segment qui est le double du deuxième, je vois apparaître une progression
croissante, qui peut continuer indéfiniment.

Cette progression est multiplicative, c'est à dire que
chaque nombre de la série est le résultat de la multiplication du nombre
précédent par le rapport (ou raison), en l'occurrence 2. Une telle progression
est aussi appelée progression géométrique.
A ce stade, on peut déjà comprendre ce que sera le travail
du facteur d'orgues qui veut mettre un buffet en proportion. Ayant choisi
une proportion, il n'a qu'à en dessiner la progression et n'utiliser dans
son dessin que des longueurs qui en font partie. Voyez ci-dessous le dessin
du buffet de l’orgue de
St-Paul à Lausanne. Les lignes horizontales au sommet du dessin sont les
longueurs utilisées.

Voyons maintenant, à l'aide de figures géométriques,
quelques proportions employées couramment dans la pratique.
Prenons un carré. Si l'on considère ses côtés, on trouve un
rapport de 1/1, qui n'offre aucune possibilité de mouvement croissant ou
décroissant. Traçons maintenant sa diagonale. Celle-ci introduit dans la figure
une nouvelle proportion :
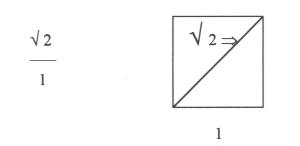
(La longueur de la diagonale se trouve par le théorème de Pythagore :
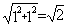 ).
).
L'application pratique la plus courante de cette proportion
est le format des feuilles de papier (A4, par exemple). On l'obtient simplement
en rapportant la diagonale du carré sur l'un des côtés.
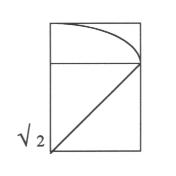
La particularité bien connue de ce rectangle de rapport  est qu'il se partage
dans la longueur en deux petits rectangles de même rapport. En effet, leur
rapport est de
est qu'il se partage
dans la longueur en deux petits rectangles de même rapport. En effet, leur
rapport est de 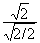 ce qui se résout en
ce qui se résout en
 .
.

Une autre proportion issue du carré, certainement la plus
connue et la plus utilisée aussi bien par la nature que par les hommes, est
appelée section dorée, divine proportion ou nombre d'or (symbolisé par la
lettre 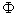 ). Prenons un carré et partageons-le en deux rectangles égaux.
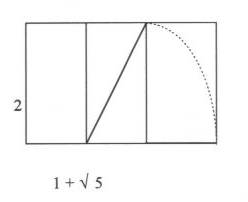
Si le côté du carré vaut 2, la diagonale du rectangle vaut
). Prenons un carré et partageons-le en deux rectangles égaux.
Si le côté du carré vaut 2, la diagonale du rectangle vaut  .
.

En rabattant cette diagonale sur le côté du carré, on obtient
un rectangle appelé rectangle d'or, dont le rapport vaut  .
.
Le nombre d'or a de nombreuses propriétés, dont la
principale se résume par l'équation suivante:
 .
.
Les conséquences de cette équation peuvent se voir en considérant
une progression de rapport 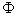 dans laquelle, chaque
nombre étant obtenu par multiplication du nombre précédent par
dans laquelle, chaque
nombre étant obtenu par multiplication du nombre précédent par  , si le premier vaut 1, le deuxième vaut
, si le premier vaut 1, le deuxième vaut  , le troisième
, le troisième 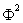 , le quatrième
, le quatrième 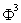 etc.
etc.
On observe que, en vertu de l'équation énoncée plus haut,
chaque terme de la série est aussi le résultat de l'addition des deux termes
précédents.

Cette série a donc le privilège d'être à la fois
multiplicative et additive (elle est en même temps une progression géométrique
et une série arithmétique).
Il existe une approximation de la section dorée par termes
entiers dans la série de Fibonaci. Chaque terme est trouvé par l'addition des
deux précédents, par exemple 1 + 1 = 2 + 1 = 3 + 2 = 5 etc.
1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21
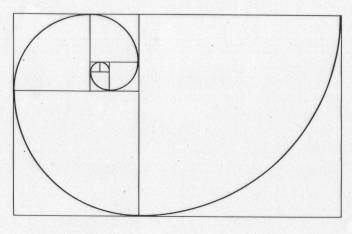
Le nombre d'or se retrouve dans différentes figures
géométriques. Dans le pentagone, il est (entre autres) le rapport entre la
diagonale et le côté. Dans le décagone, c'est le rapport entre le côté et le
rayon du cercle circonscrit. Le décagone symbolisait souvent le macrocosme, les
deux figure pouvant s'inscrire l'une dans l'autre.
Dans la nature, le nombre d'or et les constructions dérivées
du pentagone se trouvent abondamment, principalement chez les êtres vivants
(animaux ou plantes), alors que les minéraux, les cristaux, etc. se
construisent principalement sur le carré, l'hexagone etc.
On trouve une autre proportion dans le triangle équilatéral,
dans le rapport qui existe entre la base et la hauteur, qui vaut : 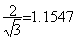

Ce rapport porte le nom de coudée sacrée. Le même rapport
existe entre le côté de ce triangle et le diamètre de son cercle circonscrit.
Le triangle équilatéral servait, entre autres, de symbole pour
exprimer les quatre éléments :
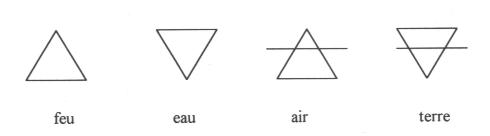
Ces quatre symboles superposés donnent le globe terrestre
dans son entier ou le sceau de Salomon :
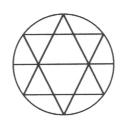
L'hexagone donne la même proportion que le triangle
équilatéral. Le côté de l'hexagone et le rayon du cercle circonscrit sont
égaux.
Pour les polygones à 7, 8 et 9 côtés, on considère toujours
le rapport entre le côté et le rayon du cercle circonscrit. Les polygones à
plus de dix côtés ne sont pratiquement pas utilisés, si ce n'est le dodécagone
(12 côtés). Son rapport côté-rayon vaut 1.9218. ce qui donne une progression
très rapide et fait presque double emploi avec rapport 2/1.
Conclusion
La mise en proportion est une ordonnance du chaos. La nature
utilise les proportions, ou s'en approche. Les Anciens, en constatant ce fait,
y ont vu une volonté divine. Ils ont donc pris la nature comme modèle. Par
cette démarche, l'homme participait par ses réalisations à la création divine
et la cultivait, précisant les choses là où la nature ne montrait qu'une
tendance. C'est dans cette pensée que les grands hommes de l'Antiquité et du
Moyen-Age travaillaient. Un homme comme J.S. Bach baignait encore complètement
dans ces idées et c'est dans cet esprit qu'il faut comprendre son insistance à
écrire Soli Deo Gloria.
On ne doit pas douter de la capacité de l'homme à intervenir
dans la nature en bien ou en mal. Ceci devient très visible actuellement où
notre civilisation est capable d'anéantir la vie ou du moins la menace déjà
très sérieusement.
On ne souffre pas tant actuellement de la technique, mais de
son utilisation dénuée de proportions.
Dans tous les cas, il est impossible d'aborder l'art ancien sans une pensée tournée vers les proportions et l'idée de l'harmonie. Notre époque aurait sûrement beaucoup à gagner en renouant avec ces principes, au fond très simples.